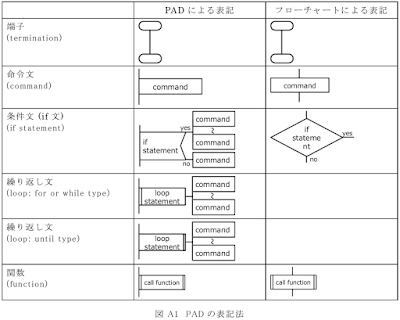
[MATLAB] 5.2 常微分方程式を解くためのプログラム
5.2 常微分方程式を解くためのプログラム
5.2.1 例題
ここでは,4.2の例題1と同じ,以下の問題を解くこととする。
$$\frac{dy}{dt}={\mu}y,{\,}y_0=y(0)=1,{\,}{\mu}=6.0,{\,}0≤t≤1 \tag{5.1}$$5.2.2 プログラム(MATLABスクリプト)
以下にプログラムを示す。
01: % (1) 計算条件設定
02: te = 1; % 計算終了時刻
03: h = 0.2; % 刻み幅
04:
05: % (2) y初期値設定
06: y = 1;
07:
08: % (3) 計算結果保存の準備
09: cnum = te / h + 1; % 計算回数
10: yr = zeros(cnum,2); % 保存用変数初期化 [t, y]
11: yr(1,:) = [0, y]; % 初期値を保存
12: k = 2; % 結果記録番号
13:
14: % (4) ループ
15: for t = 0:h:te-h
16:
17: % (5) 微分値計算
18: dydt = 6.0 * y;
19:
20: % (6) 次時刻のy計算
21: y = y + h * dydt;
22:
23: % (7) 結果を保存
24: yr(k,:) = [t+h, y];
25:
26: % (8) 結果記録番号更新
27: k = k + 1;
28:
29: end図 5.2 例題1の常微分方程式を解くためのプログラム(MATLABスクリプト)例
5.2.3 プログラムの解説
(1) 計算条件設定
ここでは,計算終了時刻 (te) と時刻の刻み幅 (h) の設定を行っている。上の例では,te = 1,h = 0.2となっており,0〜1 までの間,0.2 刻みで計算を行い,初期値の他に t = 0.2, 0.4, 0.6, 0.8, 1.0 での値が得られる設定となっている。
(2) y 初期値設定
y の初期値として 1 が設定されている。
(3) 計算結果保存の準備
ここでは,のちの繰り返し計算によって得られる y およびその時の t の値を保存する変数として yr を準備している。yr の構造を下図に示す。上の例の場合,初期値を含め合計6個の値が得られる。従って,結果を保存する変数 yr には最低6個(時刻 t も含めると12個)のデータを保存できなければならない。
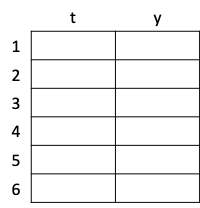
図 5.3 計算結果保存用変数 yr の構造
プログラムの9行目は,結果を保存する個数を計算している。次の10行目にある“zeros( )”とは,ゼロ行列を作成するための関数で,その大きさが (cnum)行×2列である。保存するための変数を作成すると同時に,その内容を0で初期化していることになる。
11行目では yr の1行目に t と y の初期値(それぞれ 0, 1)を代入している。
12行目の k は,次の結果を記録する yr の行を表す。
(4) ループ
15行目以降が繰り返し計算によって,所定の時間での y の値を求める箇所になる。
(5) 微分値計算
与えられた問題の微分方程式を使い,当該時刻 t での微分値を計算している。
(6) 次時刻のy計算
1次精度の方法(オイラー法)によって,次の時刻における y の値を計算している。
(7) 結果を保存
得られた結果を保存用変数 yr の k 行目に保存している。このとき,21行目で計算される y の値は次の時刻,すなわち t+h での値であることに注意。
(8) 結果記録番号更新
記録する行を一つ下に移動している。