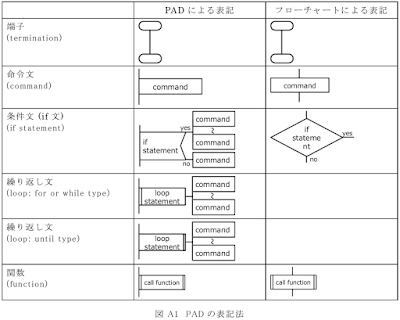
[MATLAB] 2.1 簡単な演算

-

2.1　簡単な演算

(1)　行列の作成方法

　コマンドウィンドウにて，以下のコマンドを入力する。なお “[↵]” はリターンキーを押すことを表す。

A=[1,2,3; 4,5,6; 7,8,9] [↵]

リターンキーを押すと，コマンドウィンドウに次のような結果が出力される。

>> A=[1,2,3; 4,5,6; 7,8,9]
A =
     1     2     3
     4     5     6
     7     8     9

図 2.1　コマンド入力の結果(1)

　“>>” で始まる行は，入力したコマンドを表し，その下が結果を表す。MATLABでは [　] で区切られた情報は行列1として認識される。また，行列の要素の区切りはカンマ (,) で，行の区切りはセミコロン (;) で表される。つまり，上の例では3行×3列の行列を入力しており，1行目の要素が 1, 2, 3である。結果には3行3列の行列Aが作成されたことが示されている。

　次に，以下のコマンドを入力する。

B=magic(3) [↵]

　結果は次の通りとなる。

>> B=magic(3)
B =
     8     1     6
     3     5     7
     4     9     2

図 2.2　コマンド入力の結果(2)

　この例で使用した “magic( )” という命令は，「魔方陣2」を作成しなさいという命令で，括弧内の数字は魔方陣の大きさを表す。今回の場合，3行×3列の魔方陣を作成しなさい，ということになる。結果は変数Bに格納される。

　なお，今回使用した “magic( )” のように，ある条件を与えたときにその条件に応じてあらかじめ決められた演算を行うプログラムのことを「関数 (function)」という。今回の場合，“3” が条件で，これにもとづき3×3の魔方陣が作成されている。関数の使い方はヘルプで確認できる。“magic( )”について確認したものが以下である：

>> help magic
magic  Magic square.
    magic(N) is an N-by-N matrix constructed from the integers
    1 through N^2 with equal row, column, and diagonal sums.
    Produces valid magic squares for all N > 0 except N = 2.

    Reference page for magic

図 2.3　関数“magic( )”のヘルプ内容

　MATLABには多数の関数が用意されている3。また，自分自身で新たな関数を作成し，MATLABに新たな機能を追加していくことができる。

(2)　行列の演算

　次に，簡単な演算の例を示す。MATLABは行列計算が行えることが特徴である。先の例で作成した3行×3列の行列A，Bを使い，演算の例を示す。まず，加減算の例を以下に示す。2つの行列の和 (A+B)，差 (A−B) が計算され，それらの結果がS1，M1に格納されている。

>> S1=A+B
S1 =
     9     3     9
     7    10    13
    11    17    11

>> M1=A-B
M1 =
    -7     1    -3
     1     0    -1
     3    -1     7

図 2.4　行列の加減算

　次に，積の例を示す。

>> P1=A*B
P1 =
    26    38    26
    71    83    71
   116   128   116

>> P2=A.*B
P2 =
     8     2    18
    12    25    42
    28    72    18

図 2.5　行列の積

　ここでは “A*B” と “A.*B” の2つの例を示している。両者で結果は異なる。前者は通常の行列の積となっているが，後者は「要素ごと」の積になっている。“.” は「要素ごと」という意味である。

　次に商の例を示す。積の場合と同様，“.” がついた場合は要素ごとの商となっている4。

>> D1=A/B
D1 =
   -0.0333    0.4667   -0.0333
    0.1667    0.6667    0.1667
    0.3667    0.8667    0.3667

>> D2=A./B
D2 =
    0.1250    2.0000    0.5000
    1.3333    1.0000    0.8571
    1.7500    0.8889    4.5000

図 2.6　行列の商

(3) 結果表示の省略

　ここまでに示した例では，コマンドの結果を逐一確認してきた。しかし，実際に使用する際には結果を表示させたくない場合がある。そのような場合，コマンドの最後にセミコロン (;) を付けて実行する。

  1. ベクトルを含む。 ↩︎
  2. 魔方陣とは，縦方向・横方向・斜め方向のいずれでも，1つの列の和が同じ行列をいう。 ↩︎
  3. 関数の一覧は，例えば次のページなどで確認できる：

    https://jp.mathworks.com/help/matlab/referencelist.html?type=function&s_cid=doc_ftr ↩

  4. “/B” はBの逆行列をかけることを意味し，“* inv(B)”と同じである。 ↩︎

このブログの人気の投稿

[MATLAB] 2.3 行列の要素を抽出する

-
2.3　行列の要素を抽出する 　5行×5列の行列を使い，行列の一部を抽出する例を示す。 (1)　1要素のみ >> C=magic(5) C = 17 24 1 8 15 23 5 7 14 16 4 6 13 20 22 10 12 19 21 3 11 18 25 2 9 >> C(2,4) ans = 14 図 2.10　行列要素の抽出例(1) 　上の例で “C(2,4)” は，「Cの2行目4列目の要素」を意味する。このように，MATLABにおいて行列要素の表記は「行列名（行,列）」となっている。 (2)　行要素全て >> C(1,:) ans = 17 24 1 8 15 図 2.11　行列要素の抽出例(2) 　“C(1,:)” は，「Cの1行目の要素全て」を意味する。括弧内の “1” が1行目，“:” は全ての列要素であることを示している。 (3) 列要素全て >> C(:,1) ans = 17 23 4 10 11 図 2.12　行列要素の抽出例(3) 　こちらの例では先の例と括弧内の順序が異なっており，1列目のみが抽出される。 (4)　複数の行要素全て 　次の例では，2行目と4行目の要素を全て抽出している。行の指定において “[2,4]” とすることで，同時に2つの行を指定している。 >> C([2,4],:) ans = 23 5 7 14 16 10 12 19 21 3 図 2.13　行列要素の抽出例(4) 　次の例では，行の指定を “2:5” としている。この場合，「2から5までの整数」という意味になる。つまり，2, 3, 4, 5行目を指定していることになる。 >> C(2:5,:) ans = 23 5 7 14 16
続きを読む

[MATLAB] A1 PAD (Problem Analysis Diagram)

-
イメージ
A1　PAD (Problem Analysis Diagram) 　プログラムの構造（アルゴリズム）を示す方法としてフローチャートが有名である。フローチャートは自由度が高く複雑な構造を表すことができる。しかしその一方で，複雑な構造になるほど線の数がおおくなり，プログラム構造が見にくくなる問題点がある。また，同じ構造でも違う図式で書けてしまうという問題点もある。 　PAD は，1979年に開発された方法で，プログラムの構造が見やすい，図式からのコーディングが容易であるなどの特長を有する 1 。 図 A1　PADの表記法 　例として，1から10までの整数の和を計算し，足している数が奇数なら“odd number”，偶数なら“even number”と出力するプログラムと，それをPADで表したものを示す。PADにおいて，プログラムは上方から下方に向けて処理が実行されることを示している。 total=0; 　… ① for i=1:10　… ② total = total + i; 　… ③ if (rem(i,2)==1) 　… ④ disp('odd number'); 　… ⑤ else disp('even number'); 　… ⑥ end end disp(total); 　… ⑦ 図 A2　サンプルプログラム 図 A3　サンプルプログラムのPAD 二村良彦, 1986. PADの開発. 日立評論 5, 7-11. ↩︎
続きを読む

[MATLAB] 3.3 解析

-
イメージ
3.3　解析 　ここでは，水温と溶存酸素濃度 (DO) との間に相関関係があるかどうかを確認してみる。 (1)　水温とDOとの関係をグラフで確認する 1) 全てのデータでグラフを作成する plot(WT(:),DO(:),'o'); xlabel('WT'); ylabel('DO'); [↵] 図 3.3　水温とDOとの関連性 　データはばらついているものの，水温とDOとの間にはなんらかの関係がありそうな雰囲気がある。ただ，この図では全ての水深のデータを一度にプロットしているので，傾向がはっきりしない。 2) 水深ごとに色を変えて表示してみる plot(WT,DO,'o'); xlabel('WT'); ylabel('DO'); [↵] legend(['01'; '02'; '03'; '04'; '05'; '06'; '07'; '08'; '09'; '10']) ; [↵] 図 3.4　水温とDOとの関連性 （水深別に色分け） 　水温とDOとの関係は，水深によってはっきりと異なること，水深によっては水温とDOとの間に相関関係がありそうなことがわかる。 3) 水深ごとに別々のグラフを作成する for k=1:10, subplot(4,3,k); plot(WT(:,k),DO(:,k),'o'); title(num2str(k)); end [↵] 図 3.5　水深ごとの水温とDOとの関連性 　水深の浅い地点で，水温とDOとの間に負の相関関係がはっきりと表れている。 (2)　相関係数を確認する 1) 相関関係を求める 　最も浅い水深での水温とDOとの相関係数を求めてみる： corrcoef(WT(:,1), DO(:,1)) [↵] → 以下の通り出力される。ansの1行目1列目，2行目2列目はそれぞれWT(:,1)，DO(:,1)同士の相関係数で，通常は1になる。1行目2列目，2行目1列目が
続きを読む