資料おきば [NH]

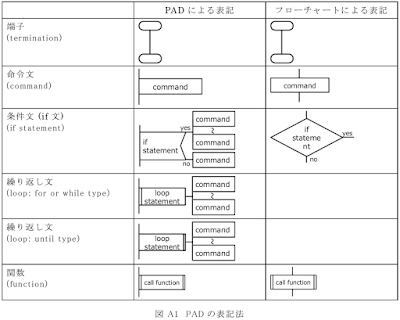
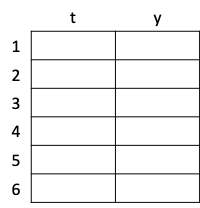
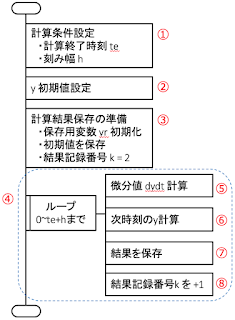
A1　PAD (Problem Analysis Diagram) 　プログラムの構造（アルゴリズム）を示す方法としてフローチャートが有名である。フローチャートは自由度が高く複雑な構造を表すことができる。しかしその一方で，複雑な構造になるほど線の数がおおくなり，プログラム構造が見にくくなる問題点がある。また，同じ構造でも違う図式で書けてしまうという問題点もある。 　PAD は，1979年に開発された方法で，プログラムの構造が見やすい，図式からのコーディングが容易であるなどの特長を有する 1 。 図 A1　PADの表記法 　例として，1から10までの整数の和を計算し，足している数が奇数なら“odd number”，偶数なら“even number”と出力するプログラムと，それをPADで表したものを示す。PADにおいて，プログラムは上方から下方に向けて処理が実行されることを示している。 total=0; 　… ① for i=1:10　… ② total = total + i; 　… ③ if (rem(i,2)==1) 　… ④ disp('odd number'); 　… ⑤ else disp('even number'); 　… ⑥ end end disp(total); 　… ⑦ 図 A2　サンプルプログラム 図 A3　サンプルプログラムのPAD 二村良彦, 1986. PADの開発. 日立評論 5, 7-11. ↩︎

5.2　常微分方程式を解くためのプログラム 5.2.1　例題 　ここでは，4.2の例題1と同じ，以下の問題を解くこととする。 $$\frac{dy}{dt}={\mu}y,{\,}y_0=y(0)=1,{\,}{\mu}=6.0,{\,}0≤t≤1 \tag{5.1}$$　 5.2.2　プログラム（MATLABスクリプト） 　以下にプログラムを示す。 01: % (1) 計算条件設定 02: te = 1; % 計算終了時刻 03: h = 0.2; % 刻み幅 04: 05: % (2) y初期値設定 06: y = 1; 07: 08: % (3) 計算結果保存の準備 09: cnum = te / h + 1; % 計算回数 10: yr = zeros(cnum,2); % 保存用変数初期化 [t, y] 11: yr(1,:) = [0, y]; % 初期値を保存 12: k = 2; % 結果記録番号 13: 14: % (4) ループ 15: for t = 0:h:te-h 16: 17: % (5) 微分値計算 18: dydt = 6.0 * y; 19: 20: % (6) 次時刻のy計算 21: y = y + h * dydt; 22: 23: % (7) 結果を保存 24: yr(k,:) = [t+h, y]; 25: 26: % (8) 結果記録番号更新 27: k = k + 1; 28: 29: end 図 5.2　例題1の常微分方程式を解くためのプログラム（MATLABスクリプト）例 5.2.3　プログラムの解説 (1)　計算条件設定 　ここでは，計算終了時刻 (te) と時刻の刻み幅 (h) の設定を行っている。上の例では，te = 1，h = 0.2となっており，0〜1 までの間，0.2 刻みで計算を行い，初期値の他に t = 0.2, 0.4, 0.6, 0.8, 1.0 での値が得られる設定となっている。 (2)　y 初期値設定 　y の初期値として 1 が設定されている。 (3)　計算結果保存の準備 　ここでは，のちの繰り返し計算

　本章では，MATLABの関数を使い，常微分方程式を解く方法について学ぶ。ここでは1次精度の方法（オイラー法）を用いることとする 1 。 5.1　プログラムの全体像 　プログラムの全体像は以下の通りとする。なお，本図ではPADと呼ばれる表記法を使用している（PADについては 備考 A1 を参照）。 図 5.1　常微分方程式を解くためのプログラムの構造 　図中④の部分で時刻 (t) を 0〜te+hまで間，⑤〜⑧までの命令を繰り返し実行する。各時刻において，現在のyの値 ($y_n$) から次の時刻でのyの値 ($y_{n+1}$) をオイラー法により計算する。この計算には当該時刻での微分値 ($dy/dx$) が必要であり，これを⑤で求める。⑤の微分値を計算する部分は関数として別のファイルに用意する。⑤で得られた微分値を使い⑥で$y_{n+1}$を計算し，その結果を⑦で保存しておく。⑧では次の結果を保存する場所を設定する。 　①〜③は，④の繰り返し計算を行うための準備である。①では，計算時刻と刻み幅とを設定する。②ではyの初期値 ($t=0$での$y$の値) を設定する。③では，計算結果を記録するための変数（箱）yrを用意し，その中身を0に初期化しておく。また，次の結果を保存するための場所（結果記録番号）を用意しておく。 MATLABにはもともと常微分方程式を解くための関数（例えばode23, ode45など）が用意されている。そのため，本章で示すようなプログラムをわざわざ自分で作る必要はない。ここでは，MATLABでプログラムを作る例を示すこと，常微分方程式を解くとはどのようなことを手順として示すことを目的とし，あえて常微分方程式を解くためのプログラムを示している。 ↩︎

4.2　微分方程式の数値解法 　微分方程式の解を式の形で与えることが困難な場合がある。この場合，数値解法によって解の近似値を求めなければならない。以下，次の微分方程式初期値問題について，数値解法を紹介する。 $$\frac{dy}{dt}=f(t,y),{\,}y(t_0)=y_0 \tag{4.3}$$ 　$y(t)$ をテイラー展開すると次式となり，$y(t)$ から $y(t+h)$ を求めることができるはずである。 $$y(t+h)=y(t)+h y'(t)+\frac{h^2}{2} y''(t)+ ⋯ +R_{(n+1)}(t) \tag{4.4}$$ (1) 1次精度の近似（オイラー法） 　式(4.4)において，$h$の1次までの級数として表すと， $$y(t+h)=y(t)+h y'(t)+R_2(t) \tag{4.5}$$ であり，さらに残渣項を切り捨てて近似する。 $$y(t+h)≈y(t)+hy'(t) \tag{4.6}$$ $t = t_n，t+h = t_{n+1}，y_n = y(t_n)，y_{n+1} = y(t_{n+1})$ とおけば， $$y_{(n+1)}=y_n+h y'(t_n) \tag{4.7}$$ （例題1） 　次の微分方程式を，オイラー法を使っておきなさい。なお，刻み幅$h$は0.2とする。 $$\frac{dy}{dt}={\mu}y,{\,}y_0=y(0)=1,{\,}{\mu}=6.0,{\,}0≤t≤1$$　 　←　解は $y=y_0 e^{μt}$。 表 4.1　1次精度の方法での計算結果 図 4.1　1次精度の方法での計算結果 (2) 2次精度の近似 　オイラー法は計算精度が低く，誤差を小さくするためには刻み幅$h$を充分に小さくする必要がある。その一方，刻み幅$h$を小さくすると計算時間が長くなるという問題がある。そこで，計算精度を高めた種々の方法が考案されている。まず，2次精度の方法を示す。 　式(4.4)において，$h$の2次までの級数として表すと， $$y(t+h)=y(t)+hy'(t)+\frac{h^2}{2!} y''(t)+R_3(t)

4.1　Taylorの定理 　関数$f(t)$ が$n$回微分可能であるとき，2点$t, t+h$に対して $$f(t+h)=f(t)+\frac{h}{1!} f'(t)+\frac{h^2}{2!} f''(t)+ ⋯ +\frac{h^n}{n!} f^{(n)}(t)+R_n \tag{4.1}$$ とおけば $$R_n=\frac{f^{(n)}(a+{\theta}h)}{n!} h^n, {\,} 0<\theta<1 \tag{4.2}$$ を満足する$\theta$が存在する。

3.3　解析 　ここでは，水温と溶存酸素濃度 (DO) との間に相関関係があるかどうかを確認してみる。 (1)　水温とDOとの関係をグラフで確認する 1) 全てのデータでグラフを作成する plot(WT(:),DO(:),'o'); xlabel('WT'); ylabel('DO'); [↵] 図 3.3　水温とDOとの関連性 　データはばらついているものの，水温とDOとの間にはなんらかの関係がありそうな雰囲気がある。ただ，この図では全ての水深のデータを一度にプロットしているので，傾向がはっきりしない。 2) 水深ごとに色を変えて表示してみる plot(WT,DO,'o'); xlabel('WT'); ylabel('DO'); [↵] legend(['01'; '02'; '03'; '04'; '05'; '06'; '07'; '08'; '09'; '10']) ; [↵] 図 3.4　水温とDOとの関連性 （水深別に色分け） 　水温とDOとの関係は，水深によってはっきりと異なること，水深によっては水温とDOとの間に相関関係がありそうなことがわかる。 3) 水深ごとに別々のグラフを作成する for k=1:10, subplot(4,3,k); plot(WT(:,k),DO(:,k),'o'); title(num2str(k)); end [↵] 図 3.5　水深ごとの水温とDOとの関連性 　水深の浅い地点で，水温とDOとの間に負の相関関係がはっきりと表れている。 (2)　相関係数を確認する 1) 相関関係を求める 　最も浅い水深での水温とDOとの相関係数を求めてみる： corrcoef(WT(:,1), DO(:,1)) [↵] → 以下の通り出力される。ansの1行目1列目，2行目2列目はそれぞれWT(:,1)，DO(:,1)同士の相関係数で，通常は1になる。1行目2列目，2行目1列目が