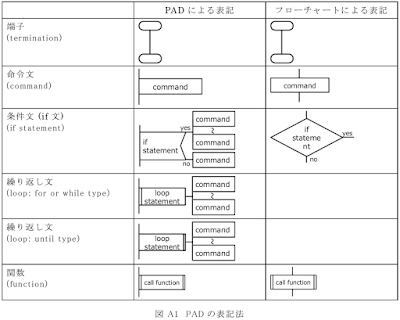
[MATLAB] 4.2 微分方程式の数値解法
4.2 微分方程式の数値解法
微分方程式の解を式の形で与えることが困難な場合がある。この場合,数値解法によって解の近似値を求めなければならない。以下,次の微分方程式初期値問題について,数値解法を紹介する。
$$\frac{dy}{dt}=f(t,y),{\,}y(t_0)=y_0 \tag{4.3}$$$y(t)$ をテイラー展開すると次式となり,$y(t)$ から $y(t+h)$ を求めることができるはずである。
$$y(t+h)=y(t)+h y'(t)+\frac{h^2}{2} y''(t)+ ⋯ +R_{(n+1)}(t) \tag{4.4}$$(1) 1次精度の近似(オイラー法)
式(4.4)において,$h$の1次までの級数として表すと,
$$y(t+h)=y(t)+h y'(t)+R_2(t) \tag{4.5}$$であり,さらに残渣項を切り捨てて近似する。
$$y(t+h)≈y(t)+hy'(t) \tag{4.6}$$$t = t_n,t+h = t_{n+1},y_n = y(t_n),y_{n+1} = y(t_{n+1})$ とおけば,
$$y_{(n+1)}=y_n+h y'(t_n) \tag{4.7}$$(例題1)
次の微分方程式を,オイラー法を使っておきなさい。なお,刻み幅$h$は0.2とする。
$$\frac{dy}{dt}={\mu}y,{\,}y_0=y(0)=1,{\,}{\mu}=6.0,{\,}0≤t≤1$$← 解は $y=y_0 e^{μt}$。
表 4.1 1次精度の方法での計算結果
図 4.1 1次精度の方法での計算結果
(2) 2次精度の近似
オイラー法は計算精度が低く,誤差を小さくするためには刻み幅$h$を充分に小さくする必要がある。その一方,刻み幅$h$を小さくすると計算時間が長くなるという問題がある。そこで,計算精度を高めた種々の方法が考案されている。まず,2次精度の方法を示す。
式(4.4)において,$h$の2次までの級数として表すと,
$$y(t+h)=y(t)+hy'(t)+\frac{h^2}{2!} y''(t)+R_3(t) \tag{4.8}$$であり,さらに残渣項を切り捨てて近似する。
$$y(t+h)≈y(t)+hy'(t)+\frac{h^2}{2!} y''(t)$$ $$→{\,}y_{n+1}=y_n+hy'(t_n)+\frac{h^2}{2!} y''(t_n) \tag{4.9}$$(例題2)
例題1の問題を,2次精度で解きなさい。
表 4.2 2次の方法での計算結果
図 4.2 2次の方法での計算結果
(3) 4次精度の近似(ルンゲ・クッタ法)
ルンゲクッタ法では,以下の式に従い$y_n$から$y_{n+1}$を計算する。
$$y_{n+1}=y_n + \frac{h}{6} (k_1+2k_2+2k_3+k_4) \tag{4.10}$$ここで,
$$k_1=g(t_n,y_n) \tag{4.11}$$ $$k_2=g(t_n +\frac{h}{2},y_n + \frac{h}{2} k_1) \tag{4.12}$$ $$k_3=g(t_n+\frac{h}{2},y_n+\frac{h}{2} k_2) \tag{4.13}$$ $$k_4=g(t_n+h,y_n+hk_3) \tag{4.14}$$であり,
$$g(t,y)=\frac{dy}{dt} \tag{4.15}$$である。
(例題3)
例題1の問題を,4次精度で解きなさい。
表 4.3 4次の方法での計算結果
図 4.3 4次の方法での計算結果