[MATLAB] 5.1 プログラムの全体像

-

　本章では，MATLABの関数を使い，常微分方程式を解く方法について学ぶ。ここでは1次精度の方法（オイラー法）を用いることとする1。

5.1　プログラムの全体像

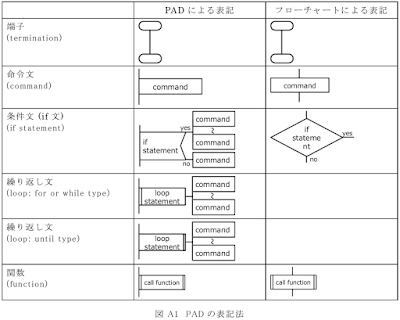
　プログラムの全体像は以下の通りとする。なお，本図ではPADと呼ばれる表記法を使用している（PADについては備考 A1を参照）。

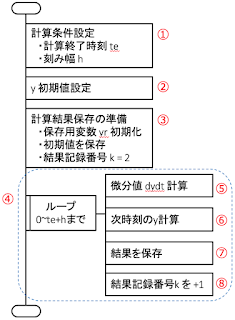
図 5.1　常微分方程式を解くためのプログラムの構造

　図中④の部分で時刻 (t) を 0〜te+hまで間，⑤〜⑧までの命令を繰り返し実行する。各時刻において，現在のyの値 ($y_n$) から次の時刻でのyの値 ($y_{n+1}$) をオイラー法により計算する。この計算には当該時刻での微分値 ($dy/dx$) が必要であり，これを⑤で求める。⑤の微分値を計算する部分は関数として別のファイルに用意する。⑤で得られた微分値を使い⑥で$y_{n+1}$を計算し，その結果を⑦で保存しておく。⑧では次の結果を保存する場所を設定する。

　①〜③は，④の繰り返し計算を行うための準備である。①では，計算時刻と刻み幅とを設定する。②ではyの初期値 ($t=0$での$y$の値) を設定する。③では，計算結果を記録するための変数（箱）yrを用意し，その中身を0に初期化しておく。また，次の結果を保存するための場所（結果記録番号）を用意しておく。

  1. MATLABにはもともと常微分方程式を解くための関数（例えばode23, ode45など）が用意されている。そのため，本章で示すようなプログラムをわざわざ自分で作る必要はない。ここでは，MATLABでプログラムを作る例を示すこと，常微分方程式を解くとはどのようなことを手順として示すことを目的とし，あえて常微分方程式を解くためのプログラムを示している。 ↩︎

このブログの人気の投稿

[MATLAB] 2.3 行列の要素を抽出する

-
2.3　行列の要素を抽出する 　5行×5列の行列を使い，行列の一部を抽出する例を示す。 (1)　1要素のみ >> C=magic(5) C = 17 24 1 8 15 23 5 7 14 16 4 6 13 20 22 10 12 19 21 3 11 18 25 2 9 >> C(2,4) ans = 14 図 2.10　行列要素の抽出例(1) 　上の例で “C(2,4)” は，「Cの2行目4列目の要素」を意味する。このように，MATLABにおいて行列要素の表記は「行列名（行,列）」となっている。 (2)　行要素全て >> C(1,:) ans = 17 24 1 8 15 図 2.11　行列要素の抽出例(2) 　“C(1,:)” は，「Cの1行目の要素全て」を意味する。括弧内の “1” が1行目，“:” は全ての列要素であることを示している。 (3) 列要素全て >> C(:,1) ans = 17 23 4 10 11 図 2.12　行列要素の抽出例(3) 　こちらの例では先の例と括弧内の順序が異なっており，1列目のみが抽出される。 (4)　複数の行要素全て 　次の例では，2行目と4行目の要素を全て抽出している。行の指定において “[2,4]” とすることで，同時に2つの行を指定している。 >> C([2,4],:) ans = 23 5 7 14 16 10 12 19 21 3 図 2.13　行列要素の抽出例(4) 　次の例では，行の指定を “2:5” としている。この場合，「2から5までの整数」という意味になる。つまり，2, 3, 4, 5行目を指定していることになる。 >> C(2:5,:) ans = 23 5 7 14 16
続きを読む

[MATLAB] A1 PAD (Problem Analysis Diagram)

-
イメージ
A1　PAD (Problem Analysis Diagram) 　プログラムの構造（アルゴリズム）を示す方法としてフローチャートが有名である。フローチャートは自由度が高く複雑な構造を表すことができる。しかしその一方で，複雑な構造になるほど線の数がおおくなり，プログラム構造が見にくくなる問題点がある。また，同じ構造でも違う図式で書けてしまうという問題点もある。 　PAD は，1979年に開発された方法で，プログラムの構造が見やすい，図式からのコーディングが容易であるなどの特長を有する 1 。 図 A1　PADの表記法 　例として，1から10までの整数の和を計算し，足している数が奇数なら“odd number”，偶数なら“even number”と出力するプログラムと，それをPADで表したものを示す。PADにおいて，プログラムは上方から下方に向けて処理が実行されることを示している。 total=0; 　… ① for i=1:10　… ② total = total + i; 　… ③ if (rem(i,2)==1) 　… ④ disp('odd number'); 　… ⑤ else disp('even number'); 　… ⑥ end end disp(total); 　… ⑦ 図 A2　サンプルプログラム 図 A3　サンプルプログラムのPAD 二村良彦, 1986. PADの開発. 日立評論 5, 7-11. ↩︎
続きを読む

[MATLAB] 3.3 解析

-
イメージ
3.3　解析 　ここでは，水温と溶存酸素濃度 (DO) との間に相関関係があるかどうかを確認してみる。 (1)　水温とDOとの関係をグラフで確認する 1) 全てのデータでグラフを作成する plot(WT(:),DO(:),'o'); xlabel('WT'); ylabel('DO'); [↵] 図 3.3　水温とDOとの関連性 　データはばらついているものの，水温とDOとの間にはなんらかの関係がありそうな雰囲気がある。ただ，この図では全ての水深のデータを一度にプロットしているので，傾向がはっきりしない。 2) 水深ごとに色を変えて表示してみる plot(WT,DO,'o'); xlabel('WT'); ylabel('DO'); [↵] legend(['01'; '02'; '03'; '04'; '05'; '06'; '07'; '08'; '09'; '10']) ; [↵] 図 3.4　水温とDOとの関連性 （水深別に色分け） 　水温とDOとの関係は，水深によってはっきりと異なること，水深によっては水温とDOとの間に相関関係がありそうなことがわかる。 3) 水深ごとに別々のグラフを作成する for k=1:10, subplot(4,3,k); plot(WT(:,k),DO(:,k),'o'); title(num2str(k)); end [↵] 図 3.5　水深ごとの水温とDOとの関連性 　水深の浅い地点で，水温とDOとの間に負の相関関係がはっきりと表れている。 (2)　相関係数を確認する 1) 相関関係を求める 　最も浅い水深での水温とDOとの相関係数を求めてみる： corrcoef(WT(:,1), DO(:,1)) [↵] → 以下の通り出力される。ansの1行目1列目，2行目2列目はそれぞれWT(:,1)，DO(:,1)同士の相関係数で，通常は1になる。1行目2列目，2行目1列目が
続きを読む